翹曲預測是射出成型模擬中的一個關鍵環節，而大多數翹曲分析都採用線性彈性法。一般情況下，模型適用線性分析，而不用考慮幾何、材料或邊界條件非線性的影響。然而有時會造成模擬結果與實驗結果不一致，尤其是對軟薄構造的模型，例如汽車產品和光學元件等。而為了改善數值模擬與實驗的差異，我們在計算中引入幾何非線性效應，詳細說明如下。

非線性結構分析

在數值結構分析中，線性彈性分析是計算在外力施加下結構變形最簡單的方法。然而在真實的實驗案例中，幾何或材料的非線性特性會顯著影響變形狀況。這些效應可能導致力和位移的非線性關係。 圖一顯示線性彈性和非線性彈性分析之平衡關係差異。

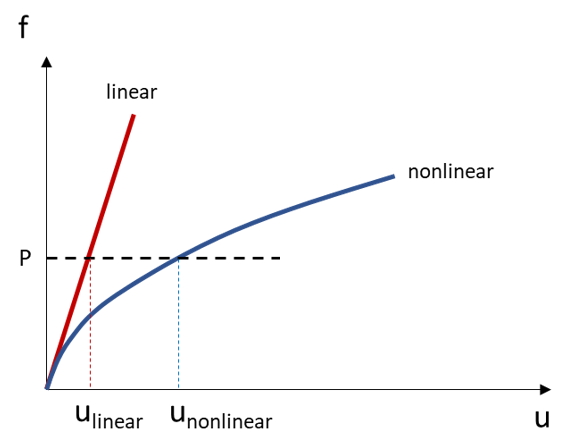
圖一 線性彈性和非線性彈性分析之平衡路徑差異

本文聚焦於幾何變化引起的非線性效應。這種非線性通常發生在厚度較小的殼狀產品，或是厚度分佈明顯不均勻的產品中。 因此，若要考慮幾何非線性效應，就必須先考量有限元變形理論。

有限元變形理論

有限元變形理論考慮了原始和變形配置之間的位置變化。因此在非線性分析中，結構剛性和邊界條件在計算過程中可能由於幾何形狀的變化而改變（不同於線性彈性分析中，剛性矩陣會維持不變）。 故結構系統可看作是位移的函數，可以表示為：

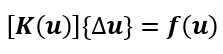
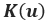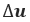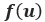此函數中，是結構剛性，是位移量，則是外力。

上述為非線性等式，我們須將其正切剛性線性化，並迭代求解。線性化後的平衡系統可以以下公式表示：

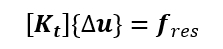
為了進行迭代計算，我們採用牛頓-拉弗森方法──解決非線性數學問題的最著名的方法。此分析會持續收斂，直到殘餘力小於收斂標準時即完成解答。

幾何擾動(Imperfection)模型應用

有時在數值分析過程中，結構分析中不容易出現非線性情況。但由於真實通常不如理想考量，模型中可能會存在製造過程產生的不完美，而這些不完美處可能會觸發非線性平衡路徑。故舉例來說，大多數數值軟體會應用微小的擾動來呈現不完美特性。我們的非線性翹曲分析中也將導入挫屈分析的特徵向量，作為觸發非線性特性的缺陷。

以「非線性翹曲分析」進行翹曲預測

Moldex3D針對使用者的翹曲分析需求，推出新的求解器「非線性翹曲分析」。在此求解器中，使用者只須選擇「非線性翹曲功能」項目，軟體進行分析時即會自動考慮非線性幾何效應。

以下先用一個簡單的例子來說明考慮幾何非線性的影響。圖二為比較「標準翹曲」和「非線性翹曲」的結果，兩個結果的變形形狀明顯不同。透過這些結果的平衡路徑，我們可以輕易觀察到該模型的幾何非線性在分析中起著重要的作用。因此若要獲得準確的分析，此類殼狀產品勢必要考慮幾何非線性的影響。

此外，非線性翹曲分析也提供應力分布結果，供使用者檢視應力值最大或應力集中的區域在何處。

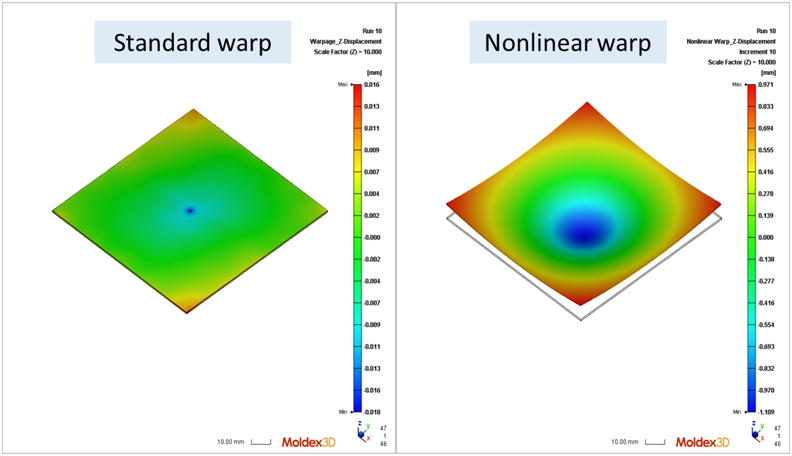
圖二 非線性翹曲分析(左)與線性翹曲分析(右)

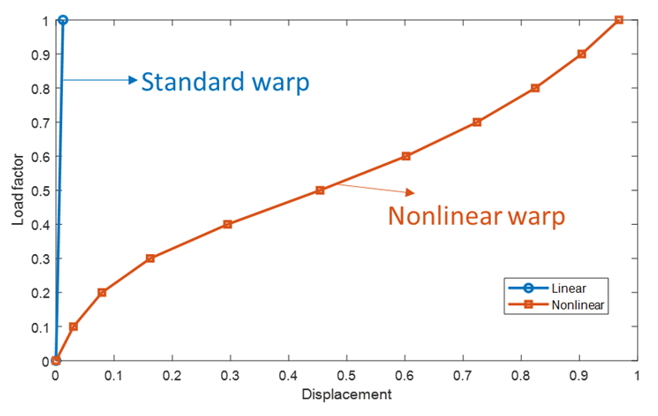
圖三 負載-位移曲線

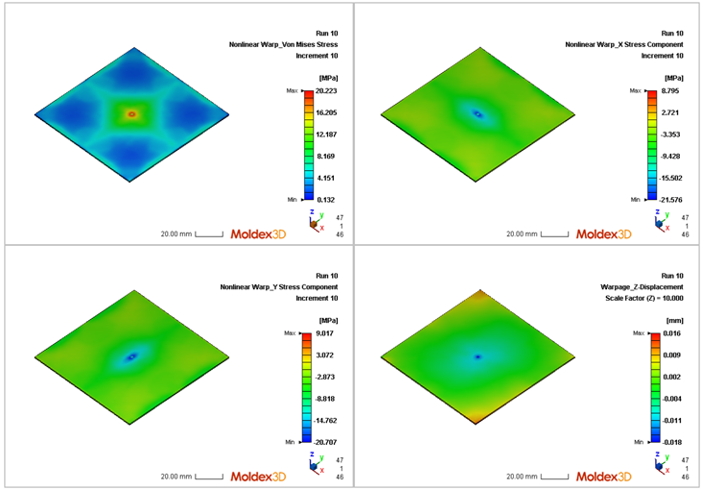
圖四 不同元件的應力分布

汽車零件應用案例

汽車零件的製造通常是以薄件或輕量化為目標，因此其幾何效應可能會導致幾何非線性及其他物理性質分布差異等問題。

以下以一個汽車零件案例來呈現幾何非線性的影響。如圖五所示，線性和非線性翹曲分析存在明顯的變形差異。圖六紅圈區域的體積收縮結果顯示，由於該區厚度較薄，使其收縮值高於其他區域。由此案例可看出，在考慮幾何非線性的情況下，顯示由模型幾何、加工條件或纖維等因素所導致的不同收縮分佈看來，對變形的影響很大。因此，對於類殼狀產品，我們通常會建議使用者選擇「非線性翹曲」分析進行變形預測。

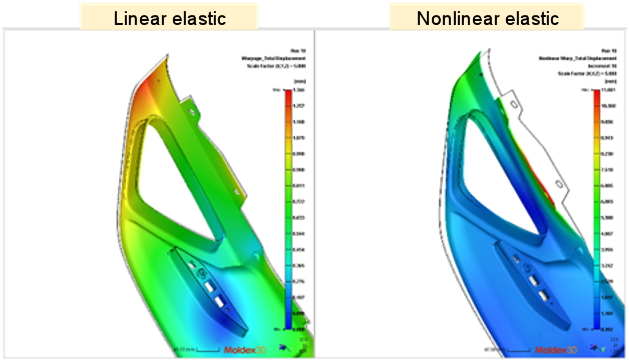
圖五 線性分析(左)與非線性分析(右)結果比較

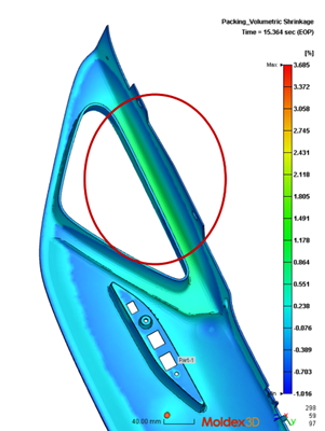
圖六 充填/保壓階段的體積收縮

簡化網格應用

迭代過程中，非線性分析非常耗時且計算成本相當高；此外，用於流動分析的網格元素數量龐大、元素形狀也較大，與結構分析的需求不同。以圖七為例，左側是原始建構的流動分析網格，但由於邊界層網格在外力施加下，網格元素可能會變形，因此有時不太適合結構分析。因此，我們通常建議使用者建構如圖七中右圖的網格，使網格元素均勻分佈。

Moldex3D在此也提供了一個介面，讓使用者可輸入元素數量和品質更適合進行結構分析的網格。透過此映射工具進一步延續射出模擬的資訊，可顯著降低計算成本，並妥善保存重要的物理量值。

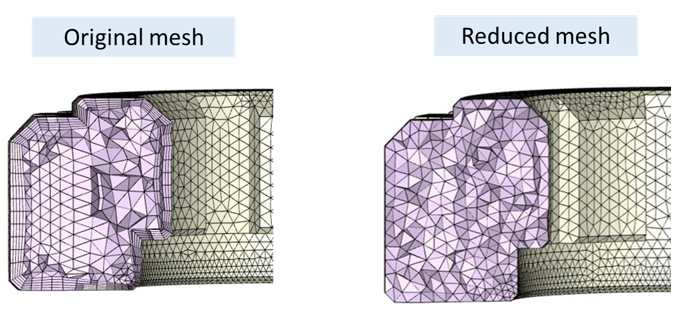
圖七 原始網格與簡化網格比較

結論

除了標準和強化版翹曲分析外，Moldex3D還提供了考慮幾何非線性的翹曲求解器。我們強烈建議使用者選擇此求解器來進行殼件產品，如汽車零件和光學元件的翹曲分析。此外，我們還提供了一個界面供用戶使用元素量較少的模型進行分析，以降低分析的總計算成本。